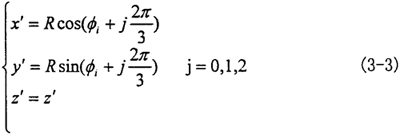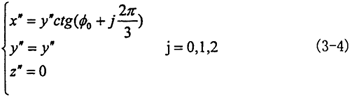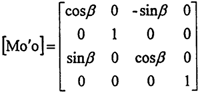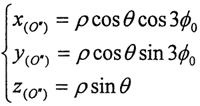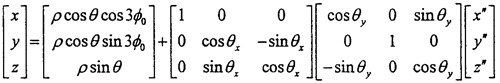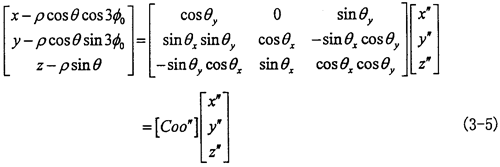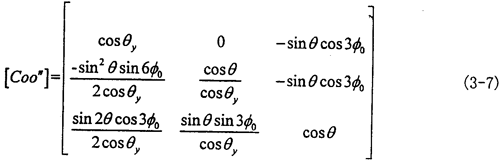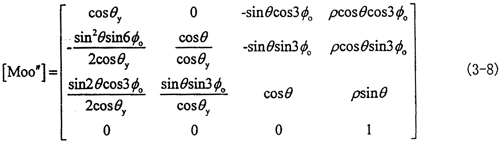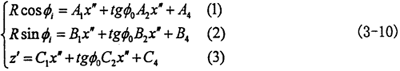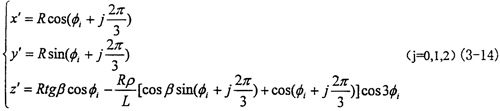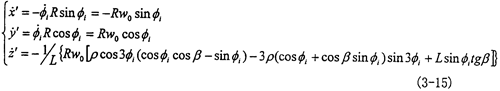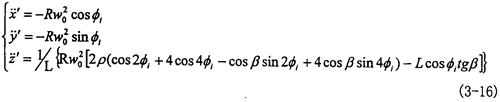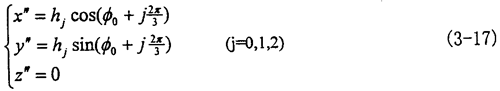3.2.4.1 聯立方程的求取
由建立的坐標系可知：
在定坐標系O′X′Y′Z′中輸入軸的三滑道軸線m1、m2、m3方程為：
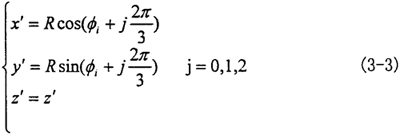
在動坐標系O″X″Y″Z″中三叉桿軸頸的軸線n1、n2、n3方程為：
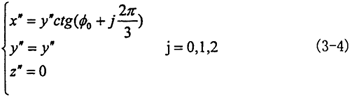
定坐標系O′X′Y′Z′與定坐標系OXYZ之間的四階變換矩陣為：
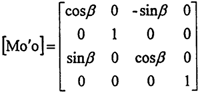
下面討論如何在固定坐標系O′X′Y′Z′中表達出三叉桿軸線的參數方程。
為求出這個參數方程，我們必須解決動坐標系O″X″Y″Z″同定坐標系OXYZ之間的坐標變換矩陣[Moo″]。
已知O″點在OXYZ中的坐標為：
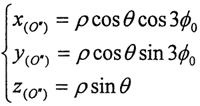
由于動坐標系O″X″Y″Z″的O″Y″軸取得始終垂直于固定坐標系OX軸，可認為先把OXYZ坐標系繞OX軸轉過夾角θx，使OY軸與O″Y″軸平行，再繞新的OY軸轉過θy，使OX軸與O″X″軸平行，OZ軸也同時平行于O″Z″軸（變換空間位置如圖3-6所示）。則固定坐標OXYZ與動坐標系間的變換關系如下：
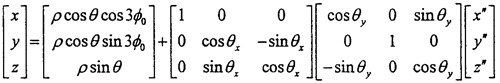
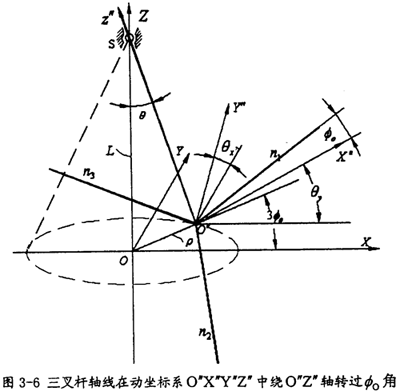
所以有：
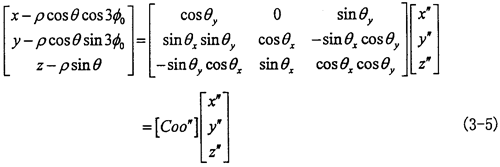
因O″Z″與OZ的交點S在OXYZ坐標系中的坐標為（O，O，L），在O″X″Y″Z″坐標系中的坐標為（O，O,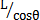
），代入式（3-5）
可推出：
由式（3-6）可知|θy|<θ，|θx|<θ一般來說θ值非常小，則θy和θx則更小。到此方向余弦矩陣[Coo″]的所有項均可求出。其具體的形式如下（為簡化書寫將θy作為已知參數代入）：
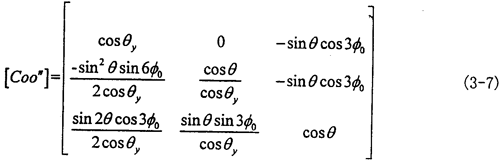
于是動坐標系O″X″Y″Z″與定坐標系OXYZ之間的四階變換矩陣[Moo″]為：
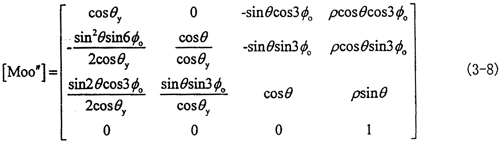
其中tgθ=
，（L為圓錐擺中軸線長，P為圓錐擺底圓半徑（見圖3-3））
又坐標系O′X′Y′Z′與坐標系O″X″Y″Z″之間的四階變換矩陣為：
[Mo′o″]=[Mo′o] [Moo″]
故三叉桿軸頸的軸線方程由坐標系O″X″Y″Z″轉到坐標系O′X′Y′Z′為：
（3-7）式中A1、A2、A3、A4、B1、B2、B3、B4、C1、C2、C3、C4等于其在矩陣[Mo′o″]中對應位置的表達式。
將式（3-3）同式（3-9）式聯立，則有：
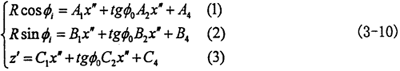
3.2.4.2 輸入、輸出轉角關系的求取
由式（3-10）中的（1）、（2）兩式，消去x″，即可求出輸入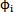角
同輸出角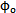
的關系。
（A1+tg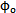·A2）sin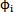-（B1+tg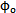·B2）cos+
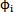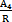（B1+tg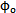·B2）-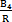
（A1+tg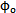·A2）=0 （3-11）
在式(3-11)中略去sinθ的平方和高次項（根據實際情況p<<L，故θ也非常小），同時令cosθy≈1（由式（3-6）可知是合理的）。則可得出輸入同輸出轉角關系：
轉角關系：-≈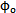
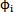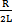tgβtg2
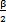cos3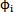(此處單位為弧度，后面的分析中轉化為度) （3-12）
速比關系：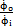
=
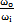≈1-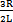
tgβtg2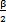sin3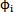（單位為弧度/秒） （3-13）
3.2.4.3 小桿的運動分析
3.2.4.3.1 小桿相對于滑道的運動
對式（3-10）中的第（3）式作近似處理sinθ≈≈0，cosθ≈1（實際上p<<L,近似處理是合理的），則可得到三小桿的球面中心P在固定坐標系O′X′Y′Z′中的運動軌跡：
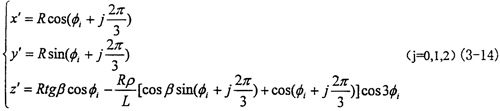
由式（3-14）則有小桿在滑道中的滑動位移即為坐標z′值，由于三小桿的滑動位移是相同的，可取其中之一進行表示，令h1為其位移量則可表示為：
h1=Rtgβcos-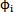
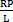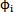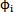[cosβsin+cos]cos3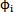
小桿球面中心P在定坐標系O′X′Y′Z′中的坐標（x′y′z′）表示成向量形式為：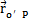
=（x′，y′，z′），將其對時間t求導得到：
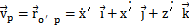，則P點的絕對速度為vp=
。
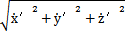其中：
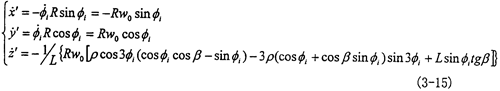
上式中作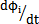
=wo=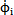
=wi的處理（三叉桿式萬向聯軸器輸入同輸出的轉角差值很小，可以認為是等角速傳動，這在后面的分析中可以證明。）
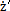=vpz是小桿沿著滑道的相對速度，將速度
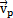再次對時間t求導可得小桿運動的加速度：
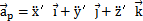（其中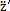
=αpz是小桿沿著滑道的相對加速度）。
假設輸入軸的轉速為定值，則ε=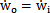
=o，此時：
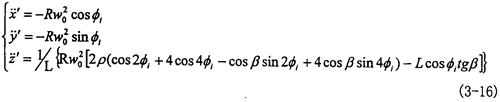
3.2.4.3.2 小桿（球面中心P）相對于三叉桿軸頸的運動小桿的球面中心P在動坐標系O″X″Y″Z″中的參數方程為：
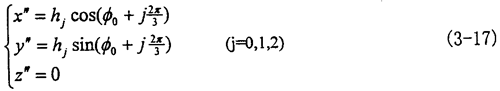
（方程中hj為小桿的球面中心P到三叉桿軸線的距離，因為三小桿運動相同，故取其中之一分析，可令j=0)
將（3-17)式代入（3-10）式中第（2）個方程可得
Rsin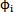=B1hocos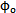+B2hosin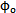+B4
由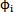=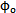，cosθ≈1，sinθ≈0則可得出小桿球面中心P沿著三叉桿軸頸相對位移量為：
ho=R-P-2Pcos2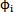 （3-18）
將位移ho對時間t求導可得小桿球面中心P沿三叉桿軸頸的相對速度：
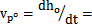4PWosin2 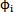（3-19）
將速度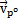
再次對時間t求導可得小桿球面中心P沿三叉桿軸頸的相對加速度：
=
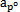=8
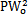cos2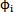 （3-20）
上一頁
下一頁
