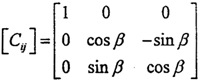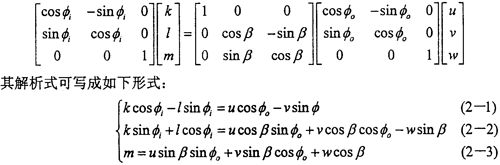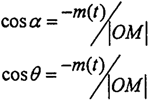分度機構剖析
環叉式萬向聯軸器實質上是由雙聯十字軸萬向聯軸器加導桿球籠式萬向聯軸器的分度機構所組成。環叉式萬向聯軸器同導桿球籠式萬向聯軸器的等角速傳動特性的好壞關鍵就是由分度機構的性能所決定。對分度機構性能的深入分析,完全解析其特點十分有意義。
在環叉式萬向聯軸器中采用的分度機構布置形式見圖2-17中紅色部分。當叉軸1相對叉軸2有偏轉時,分度機構的三個球頭分別相對它們的配合構件轉動,這樣就會帶動十字軸和十字環偏轉一定的角度。根據現有的等角速傳動理論,當十字軸和十字環偏轉的角度為叉軸1相對叉軸2偏轉角的一半時,將會把十字軸和十字環偏轉到叉軸l相對叉軸2的等分角平面,這樣傳力點就會在等分角平面內,從而實現等角速傳動。那么現在的關鍵問題是分度機構是否能正好將角度偏轉一半。作出分度機構的原理簡圖如圖2-18所示。機構中各參數的關系如下式:

m=18mm,a=9.7mm,b=27.7mm這里值的選取已經過優化)
現作出分度機構中理論半偏轉角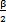 ,實際半偏轉角γ和它們的差的函數圖形,如圖2-19所示。
,實際半偏轉角γ和它們的差的函數圖形,如圖2-19所示。

在圖2-19中,可以看到, ,γ的函數圖形,在β角小于36度以前,幾乎是重疊的,在36度以后,才開始有明顯的差異,這一點從它們的差值曲線(圖2-19中下面的紫紅色曲線)也可以看出。這就是說,此機構在目前的尺度下在36度以前,它的分度性能是相當理想的,值得借鑒。不過從分度性能曲線上,可以看出,環叉式萬向聯軸器并非是完全的等角速萬向聯軸器,因為在36度以前的分度也有微小的差異。
,γ的函數圖形,在β角小于36度以前,幾乎是重疊的,在36度以后,才開始有明顯的差異,這一點從它們的差值曲線(圖2-19中下面的紫紅色曲線)也可以看出。這就是說,此機構在目前的尺度下在36度以前,它的分度性能是相當理想的,值得借鑒。不過從分度性能曲線上,可以看出,環叉式萬向聯軸器并非是完全的等角速萬向聯軸器,因為在36度以前的分度也有微小的差異。
2.3.1.2.2 THOMPSON 式萬向聯軸器
將環叉式萬向聯軸器的中間直線分度桿轉變為球面分度機構,就成為一種新型的等角速萬向聯軸器,這就是THOMPSON式萬向聯軸器其結構如圖2-20所示。
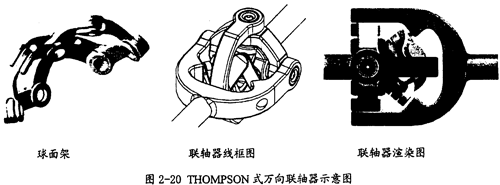
這種聯軸器中通過用球面架(圖2-20左邊)來分度,相對環叉式萬向聯軸器來說,結構上是復雜了,但它將環叉式分度中的高副全變為了低副,在潤滑上會非常優良,壽命就會大大提高。從上面的結構上看,這種改變在制造和裝配上并未帶來任何不便。據現有的實驗資料表明,這種聯軸器是一種等角速萬向聯軸器,目前這種聯軸器在國內還未見有報導。
2.3.2 定心式等角速萬向聯軸器傳動理論及其產品
2.3.2.1 定心式等角速萬向聯軸器傳動理論
定心式等角速理論
a.兩軸相交時,兩軸交點與嚙合點恒位于兩軸線所成夾角的平分面上,可實現萬向聯軸器等角速轉動(又稱同步);
b.兩軸相錯時,單一的萬向聯軸器聯接不能實現等角速轉動的目的。
理論證明如下:
萬向聯軸器的等角速條件
2.3.2.1.1 當輸入、輸出軸相交時的等角速條件
先將萬向聯軸器簡化為如圖2-21所示的數學模型。建立模型及坐標系如下:Zi和Zj分別代表輸入與輸出軸,Xi和Xj軸重合,均垂直于Zi和Zj所組成的平面。兩軸間的夾角為β。特別須說明的是,本文所建立的坐標系均為右手坐標系,為了清晰起見,Y軸一般不再標出,可根據右手定則判斷其方向。
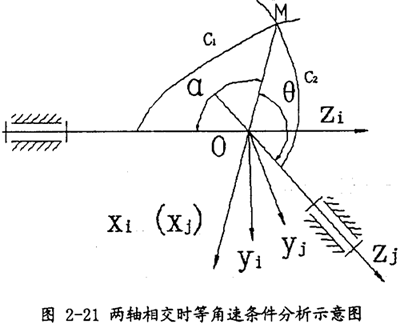
假設M點是兩軸的嚙合點(運動曲線C1和C2的交點,也就是傳力點)假設初始條件為:當時間t=0時,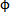 i(輸入軸轉角),
i(輸入軸轉角), 0(輸出軸轉角)均為零,在兩坐標系OXiYiZi和OXjYjZj中,曲線Cl和C2的方程分別為:
0(輸出軸轉角)均為零,在兩坐標系OXiYiZi和OXjYjZj中,曲線Cl和C2的方程分別為:

如圖2-21所示,坐標系OXjYjZj可以看作是坐標系OXiYiZi繞Xi(或Xj)旋轉了一個角β度。旋轉的方向余弦矩陣為:
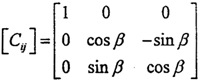
進行坐標變換有:(即由坐標系OXjYjZj變換到坐標系OXiYiZi其中(Xi,Yi,Zi),(Xj,Yj,Zj)分別表示某點在兩坐標系中的坐標。)
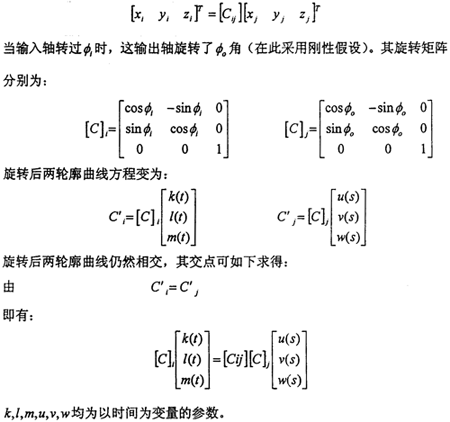
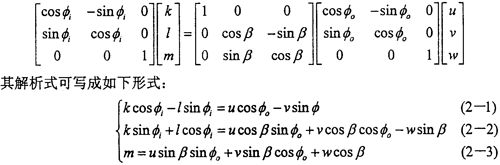
假設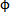 i和β角已知,上述方程中只有三個未知量(
i和β角已知,上述方程中只有三個未知量(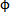 0,t,s),因此用數值方法能夠確定其解。
0,t,s),因此用數值方法能夠確定其解。
等角速條件的導出:
假設該萬向聯軸器是同步的,可令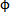 i=
i=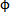 0(
0(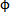 i,
i,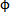 0可取任意值)
0可取任意值)
則得:

msinβ=(1-cosβ)(ksin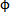 i+lcos
i+lcos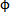 i)
i)
由于γ可在一定范圍內任意地取值,故有:
m=-w
綜合以上所述,得到聯接相交兩軸的萬向聯軸器同步性的條件為:

由于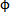 i和β的取值是任意的,交點M也是任意的,因此兩曲線方程滿足上述同步條件時,才能保證輸入、輸出是完全同步。故它們的參數方程為:
i和β的取值是任意的,交點M也是任意的,因此兩曲線方程滿足上述同步條件時,才能保證輸入、輸出是完全同步。故它們的參數方程為:

設兩曲線的交點M(嚙合點)與兩軸的交點O的連線OM與輸入軸(Zi軸的負半軸)的夾角和OM與輸出軸和夾角分別為:(在此處|OM|=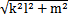 ,表示嚙合點與兩軸交點間的距離。)
,表示嚙合點與兩軸交點間的距離。)
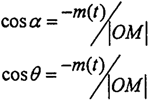
由此可得cosα=cosθ,由于0≤α≤180° 0≤θ≤180°。故有α =θ。簡而言之,兩相交軸完全同步的基本條件是:兩軸交點與嚙合點恒位于兩軸線所成夾角的平分面上。
上一頁
下一頁