第2章 等角速萬向聯軸器理論
2.1 引言
等角速萬向聯軸器機構的發明及應用開辟了萬向聯軸器的開發和應用的嶄新時代,它也是萬向聯軸器等角速運動的基礎和靈魂。對它的創新意味著有可能發明出新型的等角速萬向聯軸器,研究意義重大,萬向聯軸器機構等角速傳動的理論研究因此也成為該領域一個重要的研究課題。
實現等角速傳動,可以有多種形式。可以用高副機構也可以用低副機構,可以在兩軸間用多個構件也可以用單一構件,可以用連桿也可以用滾子或其它形狀的構件。正是由于這些不同的型式,通過型演化就會產生更多的、千變萬化的等角速機構。這也是等角速理論復雜的原因所在。
本章從等角速回轉連桿機構入手,以實際的幾種典型等角速產品為例,對不同的等角速理論進行理論推導,分析和綜合,給出了它們不同的適用范圍,為新型等角速聯軸器機構的發現提供必要的理論基礎。
2.2 等角速回轉連桿機構探討
在等角速萬向聯軸器中,大部分都屬于連桿機構.最古老的雙聯十字軸萬向聯軸器機構就是球面四連桿機構。從大量的不同的機構綜合中,有可能得出多種實用的等角速連桿機構,所以研究等角速理論,以連桿機構的型式和尺度關系為對象,進行新的等角速理論的探索,在一定的意義上是可行的。在機構學上,構件同構件間的連接稱為副,其不同的形式和代號如圖2-1所示:
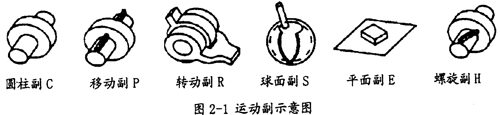
2.2.1 等角速回轉連桿機構
等角速回轉連桿機構可用于任意位置軸間的等角速傳動,如相交軸、交錯軸(interlaced shaft)、平行軸。與齒輪機構相比,它一般具有構件簡單、容易制造、傳動精度高、耐磨損等優點。現已被廣泛應用于汽車、軋鋼機等設備的雙聯十字軸萬向聯軸器、十字滑塊聯軸器等機構就是其代表。
等角速回轉連桿機構大多為空間機構,解析較繁難,其尺度約束關系式較復雜。對它的研究,只能從某些方向著手,目前我國有的學者利用基本的回轉機構等角速理論為出發點,利用機構學中型演化和運動鏈疊加等方法得出了多種具有等角速特性的機構。其理論和方法如下:
基礎理論:
若一個機構在運轉時其位形始終具有以軸交角(輸人軸和輸出軸之間的夾角)的角平分面為鏡面的對稱性,則該機構將具有等角速性。顯然,運動副與構件均對稱于上述鏡面且含有中間副的單自由度鏡面機構是這類機構的基本型式,其運動特征是,中間運動副始終在鏡面內作平面運動。這一理論直觀地闡明了一般相交軸、交錯軸等角速連桿機構的基本型式。
鏡面機構的中間運動副應始終作鏡面內的平面運動,可假想構成中間運動副的兩構件分別與鏡面構成假想平面副而形成了兩個對稱于鏡面的假想機構。稱此假想機構為“假想半聯軸器機構”。
采用的方法:
對于上述的單自由度鏡面機構,引人“假想半聯軸器機構”的概念來闡明一般相交軸、交錯軸等角速傳動連桿機構的構成型式,從而將通常十分繁難的等角速多桿空間機構尺度關系的研究,簡化為“假想半聯軸器”聯軸器機構曲柄條件的研究。應用靜力平衡法進行求解,即得出它們的曲柄存在的條件,也就得到了此機構等角速回轉的尺度約束關系式。
通過上述的方法,可以得到相交軸、交錯軸形式的多種等角速連桿機構。在圖2-2中列出了其中的一部分,它們都是相交軸傳動的形式,當然全都是鏡面機構。在這些機構中有的已被應用在等角速聯軸器上,如球鉸柱塞式萬向聯軸器就是以RPSPR機構為基礎。在圖2-3中列出了其中的一種較重要的交錯軸形式的等角速連桿機構。
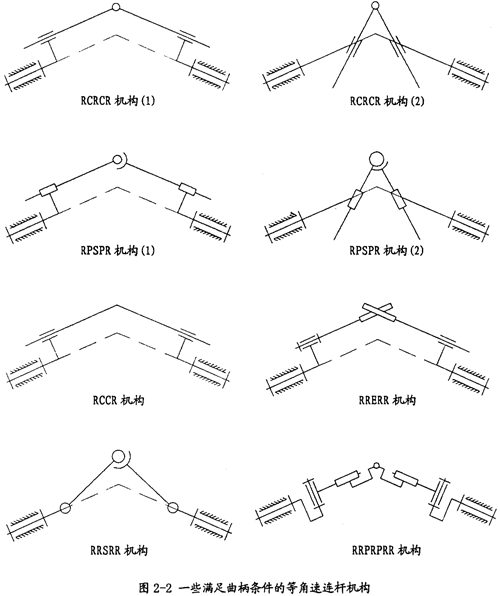
在圖2-3所示的RCRCR鏡面交錯軸等角速連桿機構中,要保證這種機構存在雙曲柄,必須滿足許多條件,圖中所示的紅色尺寸值d相等只是其中的一個,從這一約束關系,就可以看出,在等角速機構中要實現機構的等角速性能,不但需要滿足機械中各構件自身的形狀尺寸,而且也要滿足構件間的相互空間位置關系。鑒于圖2-3中所示的空間位置表達不清晰,特繪制了它的裝配模型圖和機構的各零件模型圖,分別如圖2-4、圖2-5所示。
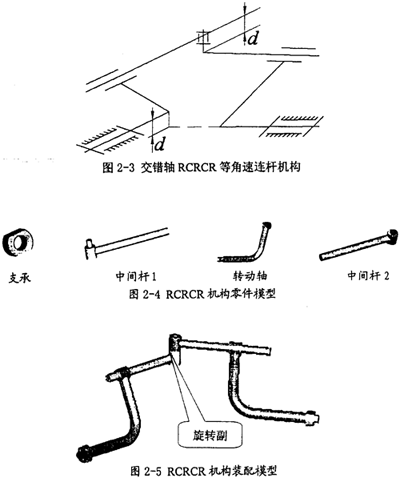
利用圖2-5中的機構形式,將其在空間中進行擴展,即可得到一種非常有價值的等角速萬向聯軸器——RCRCR交錯軸等角速萬向聯軸器。在圖2-6示意了此種聯軸器的組成零件模型,在圖2-7中示意了此種聯軸器的裝配模型,其中左右兩圖分別是從不同的視角得到的視圖。這種聯軸器在功能上能實現空間交錯軸傳動,它的主要特點是:低副結構,耐磨損性好;構件形狀簡單,便于制造;允許被聯接的兩交錯軸的偏移角變動范圍大,甚至可作直角交錯傳動(不考慮構件間干涉時)。

2.2.2 等角速連桿機構的驗證
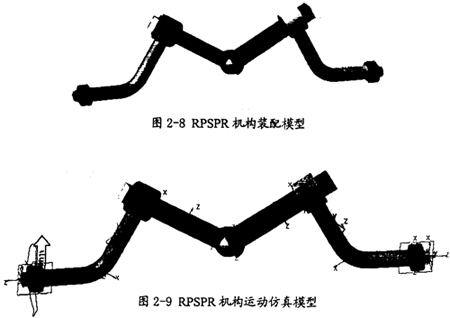
上述的理論是在鏡面機構(據現有的理論是等角速度機構)的基礎上,解出曲柄條件,得到機構等角速運動的尺寬約束關系式。為了驗證這一方法的可行性,特制作了如正氣RPSPR平面相交軸模型(如圖2-8所示),這個模型的結構左右未完全對稱(兩個移動副到球面副的距離不同)。
2.2.2.1 仿真模型的建立
在圖2-8所示模型的基礎上,通過在各構件間加上運動副,在運動副上施加運動驅動,即可得到此機構的運動仿真模型(如圖2-9所示)。在此模型的建立過程中嚴格保證各構件的共面,其運動副的形式同圖2-2中的RPSPR機構均相同。這樣在此模型中有4個構件(不含機架)、有2個旋轉副、有2個移動副、有l個球面副、模型有l個自由度,再加上l個運動驅動即可得到完整的仿真模型。不過此模型并不滿足鏡面機構的條件。
2.2.2.2 仿真結果分析
對模型進行運動仿真分析,并輸出此模型的輸入和輸出角速度的測量曲線(如圖2-10所示)。
在此仿真中共輸出了此模型運動兩周的曲線,這證明此模型中雙曲柄肯定存在,按前面的理論,如果機構是鏡面機構,在輸入轉速恒定的情況下,則輸出轉速就是恒定的,在圖2-10中,在輸入轉速恒定為90°/s時,其輸出轉速是周期變化的。后來經模型修改,將原模型改為完全對稱結構,滿足鏡面機構的條件,重新進行仿真,得出的結果是輸入轉速同輸出轉速完全相等。這從正反兩面說明了前面理論的正確性,同時也說明要想得到等角速傳動并不是一件簡單的事。不過本次證明只是對一種形式機構而言,有關其它的機構形式,還需要進一步的探索。
上一頁
下一頁





